다크프로그래머님의 글을 보고 나름대로 정리 진행한 글
지금 써진 글처럼 인용을 통해 내가 생각하는점, 추가 서술등을 작성했습니다.
카메라 캘리브레이션 (Camera Calibration) - https://darkpgmr.tistory.com/32
카메라 캘리브레이션이란
- 3차원 세상 좌표를 2차원 카메라 이미지에서 복원해야함
- 이미지상의 좌표가 실제로 3차원에서 어느좌표인가?
- “기하학적으로는” 카메라 위치, 방향
- 그러나 실제로는 렌즈, 렌즈와 센서간 거리 등 카메라 내부 기구적 요인도 크다
- 내부 기구적 요인을 제거하기 위한 intrinsic parameter를 구하는 과정이 카메라 캘리브레이션
캘리브레이션 개요
\(\begin{matrix} s \begin{bmatrix} x\\y\\1 \end{bmatrix} &=& \begin{bmatrix} f_x & skew\_cf_x & c_x\\ 0 & f_y & c_y\\ 0&0&1 \end{bmatrix} \begin{bmatrix} r_{11}& r_{12} & r_{13} & r_{14} \\ r_{21}& r_{22} & r_{23} & r_{24} \\ r_{31}& r_{32} & r_{33} & r_{34} \\ \end{bmatrix} \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} \\ &=& A[R \mid t] \begin{bmatrix} X\\Y\\Z\\1 \end{bmatrix} \end{matrix}\)
- $X,Y,Z$ - 월드 좌표계 (world coordinate system) 상 3D 점의 좌표
- $[R \mid t]$ - extrinsic parameter 월드좌표계를 카메라 좌표계로 변환하기 위한 회전 이동변환 행렬.
- 즉 카메라의 위치와 방향등 카메라와 외부공간과의 기하학적 관계에 대한 파라메터
- $A$ - intrinsic parameter 카메라 내부의 기구적 요인에 대한 파라메터
- 초점거리, aspect ratio, 중심점등
$A$ 와 $[R \mid t]$를 합쳐서 camera matrix라고 부름
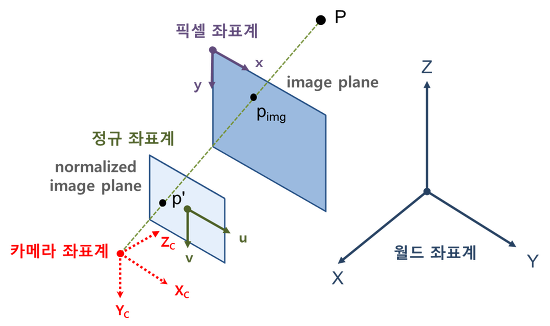
위그림은 카메라의 구조를 이미 알고있는 사람이보면 더 헷깔릴 수 있는데, 핀홀(위 그림에서 카메라 좌표계) 뒤에 있어야 하는 픽셀 좌표과와 정규 좌표계를 편의상 핀홀 앞으로 옮긴 사진임.
intrinsic parameter
카메라 내부 파라미터의 분류는 다음과 같음
- $f_x$, $f_y$ - 초점거리 focal length
- $c_x$, $c_y$ - 주점 principal point
- $skew_c$ - 비대칭계수 skew coefficient ($skew_c=tan\alpha$)
$skew_c=tan\alpha$ 가 정확히 무슨말일까요?
초점거리 forcal length
- 렌즈 중심과 이미지 센서 간의 거리
- 카메라 모델에서는 pixel 단위
- 여기서 pixel은, 이미지 센서에서의 픽셀 피치를 말함.
- 이미지 센서에서 한 픽셀당 크기가 100um고 렌즈에서 센서의 거리가 미터법으로 10mm라면 픽셀단위로는 100 pixel
- 즉, 초점거리는 센서의 픽셀 피치에 따라 상대적인 값으로 표현됨
- $f_x$, $f_y$ 로 나뉘어있는 이유는 픽셀의 피치가 가로 세로 1:1이 아닌 센서들이 있어서 그렇다. 근데 보통 1:1이니까 $f=f_x=f_y$ 로 사용해도 큰 문제 없음.
- 다른경우에는 초점거리를 센서 픽셀 피치의 가로길이, 세로길이로 각각 상대수치로 계산해서 사용
원문에는 pixel 크기라고 돼있는데, pitch가 조금 더 정확할것 같아서 픽셀 피치로 작성
- 다른경우에는 초점거리를 센서 픽셀 피치의 가로길이, 세로길이로 각각 상대수치로 계산해서 사용
normalized image coordinate
- 초점으로부터 거리 1인 지점에 가상의 평면을 생성하고, 이를 normalized image plane이라고 함
- 이 평면상에서의 좌표를 normalized image coordinate 라고 함
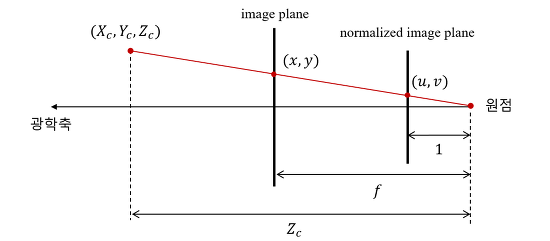
참고로 이 그림도 이미지 평면(센서)가 원점인 렌즈 앞에 가게(reflected model) 그려져있음. 실제로는 뒤로 멀어짐.
- 위 그림과 같이 카메라 좌표계에서 한점을 영상 좌표계로 변환시
- $X_c$, $Y_c$를 $Z_c$(카메라 초점과 거리)로 나누는 것이 바로 normalized image coordinate로 변환하는것.
- 여기에 다시 초점거리 $f$를 곱하면 이미지 평면에서의 영상 좌표(pixel) 이 나옴
- 그리고 이미지의 픽셀 좌표는 이미지 좌상단을 원점으로 하니까 주점인 $cx$, $cy$를 더해줘야함. 주점은 바로 다음에 설명
- 결과적으로 카메라 좌표계에서 한점을 영상 좌표계로 변환하는 식은 $(x,y)=(f_x,f_y)\frac{(X,Y)}{Z}$
카메라 좌표계가 아직 정확히 뭔지 모르겠음. 그러면 $Z_c$ 도 단위가 pixel 이겠네? 카메라 좌표도 pixel 단위?
아마도 카메라 좌표계라는것은 월드 좌표계에서 카메라 위치 기반으로 카메라의 현 위치를 원점으로 변환하고, 카메라가 바라보는 방향으로 축의 방향을 바꾼것을 말하는것같음.
주점(principal point)
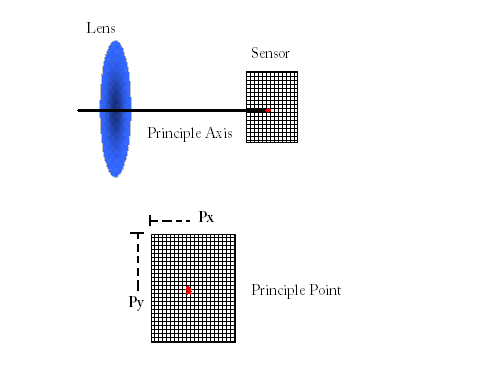출처 - https://physics.stackexchange.com/questions/11594
- 렌즈의 중심(핀홀)에서 이미지 센서에 내린 수선의 발의 영상 좌표(픽셀)
- 위 그림에서 $P_x$, $P_y$로 표현됨
- 카메라의 센서에 따라, 렌즈에 따라, 조립 과정에서의 오차에 따라 이미지센서의 중심과 렌즈의 중심이 같지 않을 수 있음